Volume 12, Issue 6 (Nov & Dec 2022)
J Research Health 2022, 12(6): 435-442 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Alikhani G, Balochian S, Khajavi A, Ziaee M. Intelligent Blood Glucose Control in Diabetic Patients by Designing and Simulating an Artificial Pancreas With a Predictive Sliding Mode Control Method. J Research Health 2022; 12 (6) :435-442
URL: http://jrh.gmu.ac.ir/article-1-2075-en.html
URL: http://jrh.gmu.ac.ir/article-1-2075-en.html
1- Department of Electrical Engineering, Gonabad Branch, Islamic Azad University of Gonabad, Gonabad, Iran.
2- Department of Electrical Engineering, Gonabad Branch, Islamic Azad University of Gonabad, Gonabad, Iran. ,saeedbalochian@gmail.com
3- Department of Community Medicine, School of Medicine, Gonabad University of Medical Sciences, Gonabad, Iran.
4- Department of Community Medicine, School of Medicine, Social Determinants of Health Research Center, Gonabad University of Medical Sciences, Gonabad, Iran
2- Department of Electrical Engineering, Gonabad Branch, Islamic Azad University of Gonabad, Gonabad, Iran. ,
3- Department of Community Medicine, School of Medicine, Gonabad University of Medical Sciences, Gonabad, Iran.
4- Department of Community Medicine, School of Medicine, Social Determinants of Health Research Center, Gonabad University of Medical Sciences, Gonabad, Iran
Full-Text [PDF 798 kb]
(462 Downloads)
| Abstract (HTML) (1734 Views)
Full-Text: (568 Views)
1. Introduction
Diabetes mellitus (DM) is one of the most common chronic diseases with various complications. The number of patients with DM in the world is estimated to be 415 million. This disease is responsible for 5 million deaths annually [1]. Insulin secreted from beta cells of the pancreas is required to transfer glucose into the cells. In type I diabetes, the immune system invades the insulin-producing cells and destroys them. Therefore, insulin delivery to obtain a normal glucose level is a key factor in the treatment of diabetes [2]. DM has no definite treatment and the patients have to cope with this disease throughout their lives. In this regard, a program should be designed to combat its complications. The malignant nature of DM is that it can threaten the health of other organs if not properly diagnosed and controlled [3].
Regulation of blood glucose levels in DM patients is one of the major aspects of medicinal systems. Researchers have recently attempted to resolve the technical problems to produce an artificial pancreas to substitute the performance of the normal and real endocrine glands of the pancreas [4]. The development of subcutaneous glucose sensors has opened new paths in controlling blood glucose levels. An artificial pancreas is composed of a series of sensors, a controller, and a subcutaneous insulin pump. The main component of this system is the control strategy adopted by the controller [5]. In this regard, the most prominent part of the artificial pancreas design is to develop a proper controller to enhance accuracy and safety.
To design a suitable controller in a system, we first need to design a model that can provide a proper description of the system. Recently, many mathematicians and researchers have modeled the medical system with differential equations [6]. These models include AIDS [7], COVID-19 [8], and blood glucose [9]. After designing the model, it is necessary to select a suitable control method and apply it to the model to achieve the desired control goals.
Various controllers have been proposed to control the insulin-blood glucose system. proportional-integral-derivative (PID) controllers [10], fuzzy PID [11], pole placement [12], resistant H control [13], predictive controller [14, 15], predictive backstepping controller [16], and adaptive control [17, 18, 19] have been employed to control the linear blood glucose systems. Numerous nonlinear strategies have been also reported based on the nonlinear models. For example, integral sliding mode control [20], type-two fuzzy backstepping control based on sliding mode observer [21], a combination of the sliding mode and backstepping [22], and predictive adaptive control [23] can be mentioned. A limited number of studies have addressed fractional-order controllers for blood glucose control among which, a fractional backstepping controller [2] and a combinational sliding mode and backstepping fractional controller [24] can be mentioned. Concerning the perturbed fractional controllers, scarce studies can be found. Disturbance and uncertainty imply glucose uptake from the foods; while time delay stands for the time taken from the insulin injection to its effects on the regulation of the blood glucose level.
To resolve the drawbacks of the previous devices, a controller should be designed that can control the fractional-order models in addition to showing resistance against the dietary disturbance (i.e. glucose absorption) and considering the delay from the insulin injection time until its uptake. Among the developed controllers, model predictive controllers (MPC) can forecast the future. A combination of MPC models with sliding mode control (SMC) can promote the model’s resistance to disturbances and uncertainty. In this context, considering the inherited features and memorial properties of fractional calculations and the advantages of MPC and SMC, the present study aims to present a hybrid controller that is a combination of sliding mode and nonlinear predictive controllers with fractional calculations to control the blood glucose considering the time delay.
2. Methods
Integer and fractional models for the blood glucose system
To control blood glucose in diabetic patients, the Bergman model or minimal fraction model is one of the best models of the blood glucose system, which consists of two parts. The first part describes the concentration of glucose in blood plasma and is independent of circulating insulin. The second part describes the concentration of insulin in the blood plasma and the middle part shows the effect of insulin on the disappearance of glucose. The minimal glucose-insulin model 1 is considered here as Equation 1 [25]:

The description of model 1 parameters is given in Table 1.
.jpg)
In model 1, d(t) shows the amount of glucose absorption from the stomach (mg/dL/min) which is considered a perturbation. This input can be considered as d(t)=Ae-(wt); w≥0; in which parameters of A and w have positive values. In most studies, A=0.5 and w=0.05. For the practical implementation of this model, it must be noted that the input of the model is the subcutaneously injected level of insulin which cannot be a negative value. Moreover, status variables such as glucose and insulin contents are physical parameters that are also non-negative.
In this study, Bergman’s model was used. Despite its simplicity, some of its complexities require the application of advanced smart control methods. Creation of a neat delay (neat delay has been also considered for converting insulin from the initial state to its absorbable form), the non-linearity of the insulin impact on the glucose, fractional order (which enhanced the modeling precision), increased uncertainty of the model (insulin uptake from the subcutaneous tissues into the blood is not a completely certain phenomenon) [26, 27], and disturbances (either due to the food consumption or disturbances in subcutaneous sensor) are some of these important features.
Although Bergman’s model has been able to provide a good description of a glucose-insulin system, due to the uncertainty of insulin absorption phenomenon and uncertainty of blood glucose range, it is not possible to accurately estimate the patient’s blood glucose parameters. To design this phenomenon, we consider this uncertainty of insulin uptake and blood glucose range in P1, P2 and P3 parameters as follows (Equation 2):
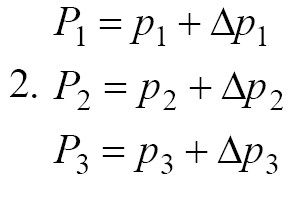
Intelligent control method
Various methods have been developed for intelligent blood glucose control which can be implemented in the present method. As this model is fractional, it can provide high precision compared to integer-order systems. On the other hand, this method included the disturbance due to food consumption and delay in insulin absorption. Hence the presented method is a predictive sliding mode control approach.
In SMC, the desired dynamic behavior can be achieved by selecting a proper sliding level; in this way, the nonlinear system can be controlled in the presence of uncertainties and disturbances. On the other hand, MPC is one of the proper techniques for controlling fractional-order, nonlinear, and delayed systems. In this method, the future behavior of the system can be predicted based on its previous behavior and its current MPC against the controlling inputs. The current controlling inputs can be then determined according to this prediction and comparing it with the control objective, i.e. stabilizing the glucose level at a specific level. This technique is specifically suitable for delayed systems. The main feature of this method is the application of an external model to predict the effect of control operation on some system outputs.
A combination of a predictive controller and a sliding mode control system can promote resistance against disturbances or uncertainties. Regarding the inherited and memorial features of the fractional calculations and the considered delay, the model provides the required predictions about the suitable amount of insulin for the patient. The combination of these two controllers to control the blood glucose level of diabetic patients has resulted in a novel unique intelligent controlling approach. In other words, in the sliding mode, the system can be controlled by selecting the appropriate sliding level depending on the dietary disturbances and nonlinearities of the blood glucose pattern; in the predictive controlling, however, the blood glucose control system is trained during the controlling process and prediction is also achieved at the same time.
Stabilization method
Stability is a crucial issue in a closed-loop control system; especially when faced with a fractional-order model with nonlinearity and uncertain parameters. Uncertainty in the parameters implies that human is a complicated system; such complex systems are not always in a single mode with definite specifications, which causes uncertainties in their parameters. Moreover, since this system is intended for human use, its instability (pulsatile or drastic insulin injection) can lead to non-compensable consequences. As a result, the control algorithm should be designed in a stable space to provide at least one intelligent observer and corrector to maintain the stability of the system. One of the ways of stability in systems is Lyapunov stability which is mentioned in [28] stability condition.
Design of the intelligent insulin injection system
The goal here is to regulate blood glucose levels to a certain level. Therefore, based on the error between the process output (glucose level) and the desired output (normal glucose level), a suitable input (required insulin) should be entered into the model. In the controller design, the body must also determine the amount of insulin injected by mathematical calculations. Today, these calculations are performed by simulation software.
Also, in this section, due to the uncertainty of blood glucose range and insulin absorption, to design a more robust predictive slip controller, we consider the uncertainty within the system with ∆p1=∆p2=∆p3=20%. Although the results may deviate from the desired point, the modeling will be more realistic and therefore a more accurate intervention. The blood glucose control system diagram is given in Figure 1. Sliding mode controller
To design a slip mode controller according to the slip mode control equations in [9], we design a sliding mode controller with u control, and then by applying the patient parameters, we obtain the level of glucose concentration and blood insulin concentration level.
Combination of a predictive controller with a sliding mode controller
To improve the performance of the sliding mode controller, with the help of predictive control that can predict the patient’s body behavior in the future, we provide a combined sliding mode control and model predictive control (SMCMPC) that has the characteristics of both controllers. (Interested researchers can contact the responsible author to obtain proofs and mathematical calculations of the controllers.)
3. Results
The simulations were carried out using MATLAB software.
Ordinary sliding mode controller for fractional-order blood glucose model (SMC)
In this situation, a sliding mode controller was employed to control the blood glucose. The initial conditions are given in model 3 (Equation 3).

Model 4 parameters were also considered (Equation 4):

, where, n=0.16 and=25 min.
In the Bergman model, a fractional order model is used to control blood glucose with time delay. In the simulation, a time delay of 25 minutes is considered, which is applied in Equation 3 of the model in x3.
Predictive sliding mode controller, sliding mode control and model predictive control (SMCMPC)
In this section, in addition to the sliding model parameters, predictive control parameters to the control algorithm in MATLAB program were considered to predict the patient’s future behavior, the prediction horizon was considered 50. Regarding the time step of 0.5 and simulation time of 500 minutes for 1000 samples, and the predictive controller loop is executed 20 times; hence the controller is computed 20 times. After 20 times, the parameters are all changed and the controller is calculated from the scratch. However, in the sliding mode control, the parameters are often constant. Uncertainty of blood glucose and injectable insulin range in each controlling area is considered to be 20%. A particle swarm optimization (PSO) algorithm was employed to optimize the objective function of the predictive controller (including mean square error and mean square of controlling attempts of u [t]) due to its proper precision. The results of both SMC and SMCMPC are presented in Figures 2 and 3. The results of both SMC and SMCMPC are discussed in the following.
4. Discussion
This study aimed to design an intelligent fractional-order predictive sliding mode controller in the presence of time delay to control blood glucose in diabetic patients. In the controller design, the performance of the glucose-insulin model should be stabilized by the controller. In the Bergmann model, the stability of glucose and insulin concentration was explored according to the system dynamics. The results showed that in the presence of a 25-minute delay, i.e. the delay from the time of insulin injection to its effect, the glucose and insulin concentration stabilized in about 60 and 50 minutes, respectively which is desirable.
For further comparison, in addition to the SMCMPC design, a conventional sliding-mode controller was designed. The conventional sliding mode controller could control the blood glucose level to the desired value, but showed huge chattering in the diagrams, reflecting instability and disturbance of glucose and insulin levels at the beginning of insulin injection. The proposed predictive sliding mode controller was able to reduce the blood glucose concentration to about 80 mg/dL in a shorter time compared to the ordinary SMC. The rate of reaching zero was higher in the SMCMPC, implying faster blood glucose regulation in diabetic patient.
Due to the uncertainty of the blood glucose and circulating insulin limits, this uncertainty in the design of controllers was considered to be 20% like the system, which results in a control design resistant to the above uncertainties, although the possible results are better without considering this uncertainty, we have designed a more accurate controller with the above design.
This research was compared with those addressing glucose-insulin model stabilization with PID controllers [10], fuzzy PID [11], pole placement [12], resistant H∞ control [13], predictive control [14, 15], predictive backstepping control [16], and adaptive control [17, 18, 19] to control linear glucose-insulin systems. Despite the satisfactory results of the mentioned methods, the linear approximation cannot fully describe the nonlinear region while the glucose-insulin system is nonlinear. Thus, the results of these controllers are not reliable and accurate. Concerning the nonlinear glucose-insulin models, such as integral sliding mode controllers [20], type-II fuzzy backstepping control based on sliding mode observer [21], a combination of sliding mode and backstepping controllers [22], and adaptive predictive control [23], it can be concluded that in all these controllers, the stability of blood glucose concentration was presented in longer than 80 minutes while this study presented a stability time of 60 minutes. Moreover, the current research considered food disturbance and delay. Other studies were on the designed controllers or resistant to food disturbance; the time delay was also included in a few cases. Therefore, the proposed system was more successful in controlling blood glucose concentration.
The intelligent blood glucose controller designed in this study has several advantages, including the use of a fractional-order model which leads to more accurate calculations and system memory. Moreover, it considered the time delay from insulin injection to its effect and explored the effect and status of hydrocarbon uptake due to food consumption. Despite the mentioned superiorities, the considered delay was a fixed value; controlling other diabetes models with the proposed controller can be considered as a future research topic by considering time-varying delays.
5. Conclusion
The combined controller of the predictive sliding model designed in this study, which is the vital part of an artificial pancreas, provides better results than previous controllers in terms of speed to normal blood glucose levels and reduces the effects of fluctuations in its amount. Better control of diabetes mellitus can reduce the complications of the disease, improve the quality of life of patients and reduce the costs for the individual and the health system.
Ethical Considerations
Compliance with ethical guidelines
There were no ethical considerations to be considered in this research.
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgments
The author appreciates the Department of Community Medicine, School of Medicine, Gonabad University of Medical Sciences.
References
Diabetes mellitus (DM) is one of the most common chronic diseases with various complications. The number of patients with DM in the world is estimated to be 415 million. This disease is responsible for 5 million deaths annually [1]. Insulin secreted from beta cells of the pancreas is required to transfer glucose into the cells. In type I diabetes, the immune system invades the insulin-producing cells and destroys them. Therefore, insulin delivery to obtain a normal glucose level is a key factor in the treatment of diabetes [2]. DM has no definite treatment and the patients have to cope with this disease throughout their lives. In this regard, a program should be designed to combat its complications. The malignant nature of DM is that it can threaten the health of other organs if not properly diagnosed and controlled [3].
Regulation of blood glucose levels in DM patients is one of the major aspects of medicinal systems. Researchers have recently attempted to resolve the technical problems to produce an artificial pancreas to substitute the performance of the normal and real endocrine glands of the pancreas [4]. The development of subcutaneous glucose sensors has opened new paths in controlling blood glucose levels. An artificial pancreas is composed of a series of sensors, a controller, and a subcutaneous insulin pump. The main component of this system is the control strategy adopted by the controller [5]. In this regard, the most prominent part of the artificial pancreas design is to develop a proper controller to enhance accuracy and safety.
To design a suitable controller in a system, we first need to design a model that can provide a proper description of the system. Recently, many mathematicians and researchers have modeled the medical system with differential equations [6]. These models include AIDS [7], COVID-19 [8], and blood glucose [9]. After designing the model, it is necessary to select a suitable control method and apply it to the model to achieve the desired control goals.
Various controllers have been proposed to control the insulin-blood glucose system. proportional-integral-derivative (PID) controllers [10], fuzzy PID [11], pole placement [12], resistant H control [13], predictive controller [14, 15], predictive backstepping controller [16], and adaptive control [17, 18, 19] have been employed to control the linear blood glucose systems. Numerous nonlinear strategies have been also reported based on the nonlinear models. For example, integral sliding mode control [20], type-two fuzzy backstepping control based on sliding mode observer [21], a combination of the sliding mode and backstepping [22], and predictive adaptive control [23] can be mentioned. A limited number of studies have addressed fractional-order controllers for blood glucose control among which, a fractional backstepping controller [2] and a combinational sliding mode and backstepping fractional controller [24] can be mentioned. Concerning the perturbed fractional controllers, scarce studies can be found. Disturbance and uncertainty imply glucose uptake from the foods; while time delay stands for the time taken from the insulin injection to its effects on the regulation of the blood glucose level.
To resolve the drawbacks of the previous devices, a controller should be designed that can control the fractional-order models in addition to showing resistance against the dietary disturbance (i.e. glucose absorption) and considering the delay from the insulin injection time until its uptake. Among the developed controllers, model predictive controllers (MPC) can forecast the future. A combination of MPC models with sliding mode control (SMC) can promote the model’s resistance to disturbances and uncertainty. In this context, considering the inherited features and memorial properties of fractional calculations and the advantages of MPC and SMC, the present study aims to present a hybrid controller that is a combination of sliding mode and nonlinear predictive controllers with fractional calculations to control the blood glucose considering the time delay.
2. Methods
Integer and fractional models for the blood glucose system
To control blood glucose in diabetic patients, the Bergman model or minimal fraction model is one of the best models of the blood glucose system, which consists of two parts. The first part describes the concentration of glucose in blood plasma and is independent of circulating insulin. The second part describes the concentration of insulin in the blood plasma and the middle part shows the effect of insulin on the disappearance of glucose. The minimal glucose-insulin model 1 is considered here as Equation 1 [25]:

The description of model 1 parameters is given in Table 1.
.jpg)
In model 1, d(t) shows the amount of glucose absorption from the stomach (mg/dL/min) which is considered a perturbation. This input can be considered as d(t)=Ae-(wt); w≥0; in which parameters of A and w have positive values. In most studies, A=0.5 and w=0.05. For the practical implementation of this model, it must be noted that the input of the model is the subcutaneously injected level of insulin which cannot be a negative value. Moreover, status variables such as glucose and insulin contents are physical parameters that are also non-negative.
In this study, Bergman’s model was used. Despite its simplicity, some of its complexities require the application of advanced smart control methods. Creation of a neat delay (neat delay has been also considered for converting insulin from the initial state to its absorbable form), the non-linearity of the insulin impact on the glucose, fractional order (which enhanced the modeling precision), increased uncertainty of the model (insulin uptake from the subcutaneous tissues into the blood is not a completely certain phenomenon) [26, 27], and disturbances (either due to the food consumption or disturbances in subcutaneous sensor) are some of these important features.
Although Bergman’s model has been able to provide a good description of a glucose-insulin system, due to the uncertainty of insulin absorption phenomenon and uncertainty of blood glucose range, it is not possible to accurately estimate the patient’s blood glucose parameters. To design this phenomenon, we consider this uncertainty of insulin uptake and blood glucose range in P1, P2 and P3 parameters as follows (Equation 2):
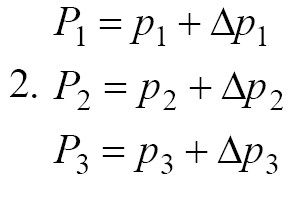
Intelligent control method
Various methods have been developed for intelligent blood glucose control which can be implemented in the present method. As this model is fractional, it can provide high precision compared to integer-order systems. On the other hand, this method included the disturbance due to food consumption and delay in insulin absorption. Hence the presented method is a predictive sliding mode control approach.
In SMC, the desired dynamic behavior can be achieved by selecting a proper sliding level; in this way, the nonlinear system can be controlled in the presence of uncertainties and disturbances. On the other hand, MPC is one of the proper techniques for controlling fractional-order, nonlinear, and delayed systems. In this method, the future behavior of the system can be predicted based on its previous behavior and its current MPC against the controlling inputs. The current controlling inputs can be then determined according to this prediction and comparing it with the control objective, i.e. stabilizing the glucose level at a specific level. This technique is specifically suitable for delayed systems. The main feature of this method is the application of an external model to predict the effect of control operation on some system outputs.
A combination of a predictive controller and a sliding mode control system can promote resistance against disturbances or uncertainties. Regarding the inherited and memorial features of the fractional calculations and the considered delay, the model provides the required predictions about the suitable amount of insulin for the patient. The combination of these two controllers to control the blood glucose level of diabetic patients has resulted in a novel unique intelligent controlling approach. In other words, in the sliding mode, the system can be controlled by selecting the appropriate sliding level depending on the dietary disturbances and nonlinearities of the blood glucose pattern; in the predictive controlling, however, the blood glucose control system is trained during the controlling process and prediction is also achieved at the same time.
Stabilization method
Stability is a crucial issue in a closed-loop control system; especially when faced with a fractional-order model with nonlinearity and uncertain parameters. Uncertainty in the parameters implies that human is a complicated system; such complex systems are not always in a single mode with definite specifications, which causes uncertainties in their parameters. Moreover, since this system is intended for human use, its instability (pulsatile or drastic insulin injection) can lead to non-compensable consequences. As a result, the control algorithm should be designed in a stable space to provide at least one intelligent observer and corrector to maintain the stability of the system. One of the ways of stability in systems is Lyapunov stability which is mentioned in [28] stability condition.
Design of the intelligent insulin injection system
The goal here is to regulate blood glucose levels to a certain level. Therefore, based on the error between the process output (glucose level) and the desired output (normal glucose level), a suitable input (required insulin) should be entered into the model. In the controller design, the body must also determine the amount of insulin injected by mathematical calculations. Today, these calculations are performed by simulation software.
Also, in this section, due to the uncertainty of blood glucose range and insulin absorption, to design a more robust predictive slip controller, we consider the uncertainty within the system with ∆p1=∆p2=∆p3=20%. Although the results may deviate from the desired point, the modeling will be more realistic and therefore a more accurate intervention. The blood glucose control system diagram is given in Figure 1. Sliding mode controller
To design a slip mode controller according to the slip mode control equations in [9], we design a sliding mode controller with u control, and then by applying the patient parameters, we obtain the level of glucose concentration and blood insulin concentration level.
Combination of a predictive controller with a sliding mode controller
To improve the performance of the sliding mode controller, with the help of predictive control that can predict the patient’s body behavior in the future, we provide a combined sliding mode control and model predictive control (SMCMPC) that has the characteristics of both controllers. (Interested researchers can contact the responsible author to obtain proofs and mathematical calculations of the controllers.)
3. Results
The simulations were carried out using MATLAB software.
Ordinary sliding mode controller for fractional-order blood glucose model (SMC)
In this situation, a sliding mode controller was employed to control the blood glucose. The initial conditions are given in model 3 (Equation 3).

Model 4 parameters were also considered (Equation 4):

, where, n=0.16 and=25 min.
In the Bergman model, a fractional order model is used to control blood glucose with time delay. In the simulation, a time delay of 25 minutes is considered, which is applied in Equation 3 of the model in x3.
Predictive sliding mode controller, sliding mode control and model predictive control (SMCMPC)
In this section, in addition to the sliding model parameters, predictive control parameters to the control algorithm in MATLAB program were considered to predict the patient’s future behavior, the prediction horizon was considered 50. Regarding the time step of 0.5 and simulation time of 500 minutes for 1000 samples, and the predictive controller loop is executed 20 times; hence the controller is computed 20 times. After 20 times, the parameters are all changed and the controller is calculated from the scratch. However, in the sliding mode control, the parameters are often constant. Uncertainty of blood glucose and injectable insulin range in each controlling area is considered to be 20%. A particle swarm optimization (PSO) algorithm was employed to optimize the objective function of the predictive controller (including mean square error and mean square of controlling attempts of u [t]) due to its proper precision. The results of both SMC and SMCMPC are presented in Figures 2 and 3. The results of both SMC and SMCMPC are discussed in the following.
4. Discussion
This study aimed to design an intelligent fractional-order predictive sliding mode controller in the presence of time delay to control blood glucose in diabetic patients. In the controller design, the performance of the glucose-insulin model should be stabilized by the controller. In the Bergmann model, the stability of glucose and insulin concentration was explored according to the system dynamics. The results showed that in the presence of a 25-minute delay, i.e. the delay from the time of insulin injection to its effect, the glucose and insulin concentration stabilized in about 60 and 50 minutes, respectively which is desirable.
For further comparison, in addition to the SMCMPC design, a conventional sliding-mode controller was designed. The conventional sliding mode controller could control the blood glucose level to the desired value, but showed huge chattering in the diagrams, reflecting instability and disturbance of glucose and insulin levels at the beginning of insulin injection. The proposed predictive sliding mode controller was able to reduce the blood glucose concentration to about 80 mg/dL in a shorter time compared to the ordinary SMC. The rate of reaching zero was higher in the SMCMPC, implying faster blood glucose regulation in diabetic patient.
Due to the uncertainty of the blood glucose and circulating insulin limits, this uncertainty in the design of controllers was considered to be 20% like the system, which results in a control design resistant to the above uncertainties, although the possible results are better without considering this uncertainty, we have designed a more accurate controller with the above design.
This research was compared with those addressing glucose-insulin model stabilization with PID controllers [10], fuzzy PID [11], pole placement [12], resistant H∞ control [13], predictive control [14, 15], predictive backstepping control [16], and adaptive control [17, 18, 19] to control linear glucose-insulin systems. Despite the satisfactory results of the mentioned methods, the linear approximation cannot fully describe the nonlinear region while the glucose-insulin system is nonlinear. Thus, the results of these controllers are not reliable and accurate. Concerning the nonlinear glucose-insulin models, such as integral sliding mode controllers [20], type-II fuzzy backstepping control based on sliding mode observer [21], a combination of sliding mode and backstepping controllers [22], and adaptive predictive control [23], it can be concluded that in all these controllers, the stability of blood glucose concentration was presented in longer than 80 minutes while this study presented a stability time of 60 minutes. Moreover, the current research considered food disturbance and delay. Other studies were on the designed controllers or resistant to food disturbance; the time delay was also included in a few cases. Therefore, the proposed system was more successful in controlling blood glucose concentration.
The intelligent blood glucose controller designed in this study has several advantages, including the use of a fractional-order model which leads to more accurate calculations and system memory. Moreover, it considered the time delay from insulin injection to its effect and explored the effect and status of hydrocarbon uptake due to food consumption. Despite the mentioned superiorities, the considered delay was a fixed value; controlling other diabetes models with the proposed controller can be considered as a future research topic by considering time-varying delays.
5. Conclusion
The combined controller of the predictive sliding model designed in this study, which is the vital part of an artificial pancreas, provides better results than previous controllers in terms of speed to normal blood glucose levels and reduces the effects of fluctuations in its amount. Better control of diabetes mellitus can reduce the complications of the disease, improve the quality of life of patients and reduce the costs for the individual and the health system.
Ethical Considerations
Compliance with ethical guidelines
There were no ethical considerations to be considered in this research.
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgments
The author appreciates the Department of Community Medicine, School of Medicine, Gonabad University of Medical Sciences.
References
- Bertachi A, Ramkissoon CM, Bondia J, Vehí J. Automated blood glucose control in type 1 diabetes: A review of progress and challenges. Endocrinología, Diabetes y Nutrición. 2018; 65(3):172-81. [DOI:10.1016/j.endien.2018.03.001]
- Heydarinejad H, Delavari H. Fractional order back stepping sliding mode control for blood glucose regulation in type I diabetes patients. In: Babiarz A, Czornik A, Klamka J, Niezabitowski M, editors. Theory and Applications of Non-Integer Order Systems. USA: Springer, Cham; 2017. [DOI:10.1007/978-3-319-45474-0_18]
- Khajehvand S, Abtahi SM. Chaotic dynamic analysis and nonlinear control of blood glucose regulation system in type 1 diabetic patients. J Adv Comp Eng Technol. 2019; 5(2):81-92. [Link]
- Saleem MU, Farman M, Ahmad A, Haque EU, Ahmad MO. A Caputo Fabrizio fractional order model for control of glucose in insulin therapies for diabetes. Ain Shams Eng J. 2020; 11(4):1309-16. [DOI:10.1016/j.asej.2020.03.006]
- Taherinasab S, Soleimaniasl S, Taherinasab S. Application of model reference adaptive control and modified Smith predictor to control blood glucose in type 1 diabetic patients. Math Comput Simul. 2021; 194:198-209. [DOI:10.1016/j.matcom.2021.05.033]
- Kilbas AA, Srivastava HM, Trujillo JJ. Theory and applications of fractional differential equations (Vol. 204). Amsterdam: Elsevier Science; 2006. [Link]
- Wang L, Li MY. Mathematical analysis of the global dynamics of a model for HIV infection of CD4+ T cells. Math Biosci. 2006; 200(1):44-57. [DOI:10.1016/j.mbs.2005.12.026] [PMID]
- Mandal M, Jana S, Nandi SK, Khatua A, Adak S, Kar TK. A model based study on the dynamics of COVID-19: Prediction and control. Chaos, Solitons, and Fractals. 2020; 136:109889. [DOI:10.1016/j.chaos.2020.109889] [PMID] [PMCID]
- Ahmad S, Ullah N, Ahmed N, Ilyas M, Khan W. Super twisting sliding mode control algorithm for developing artificial pancreas in type 1 diabetes patients. Biomedical Signal Processing and Control. 2017; 38:200-11. [DOI:10.1016/j.bspc.2017.06.009]
- Hu R, Li C. An Improved PID algorithm based on insulin-on-board estimate for blood glucose control with type 1 diabetes. Comput Math Methods Med. 2015; 2015:281589. [DOI:10.1155/2015/281589] [PMID] [PMCID]
- Yadav J, Rani A, Singh V. Performance analysis of fuzzy-PID controller for blood glucose regulation in type-1 diabetic patients. J Med Syst. 2016; 40(12):254. [DOI:10.1007/s10916-016-0602-6] [PMID]
- Nath A, Dey R, Aguilar-Avelar C. Observer based nonlinear control design for glucose regulation in type 1 diabetic patients: An LMI approach. Biomedical Signal Processing and Control. 2019; 47:7-15. [DOI:10.1016/j.bspc.2018.07.020]
- Ruiz-Velázquez E, Femat R, Campos-Delgado DU. Blood glucose control for type I diabetes mellitus: A robust tracking H∞ problem. Control Eng Pract. 2004; 12(9):1179-95. [DOI:10.1016/j.conengprac.2003.12.004]
- Magni L, Raimondo DM, Dalla Man C, De Nicolao G, Kovatchev B, Cobelli C. Model predictive control of glucose concentration in type I diabetic patients: An in silico trial. Biomed Signal Process Control. 2009; 4(4):338-46. [DOI:10.1016/j.bspc.2009.04.003]
- Abu-Rmileh A, Garcia-Gabin W. A gain-scheduling model predictive controller for blood glucose control in type 1 diabetes. IEEE Trans Biomed Eng. 2009; 57(10):2478-84. [DOI:10.1109/TBME.2009.2033663] [PMID]
- Patra AK, Mishra AK, Rout PK. Backstepping model predictive controller for blood glucose regulation in type-I diabetes patient. IETE J Res. 2020; 66(3):326-40. [DOI:10.1080/03772063.2018.1493404]
- El-Khatib FH, Jiang J, Damiano ER. Adaptive closed-loop control provides blood-glucose regulation using dual subcutaneous insulin and glucagon infusion in diabetic Swine. J Diabetes Sci Technol. 2007; 1(2):181-92. [DOI:10.1177/193229680700100208] [PMID] [PMCID]
- Tárník M, Miklovičová E, Murgaš J, Ottinger I, Ludwig T. Model reference adaptive control of glucose in type 1 diabetics: A simulation study. IFAC Proceed Vol. 2014; 47(3):5055-60. [DOI:10.3182/20140824-6-ZA-1003.00321]
- Nath A, Deb D, Dey R. Robust observer-based adaptive control of blood glucose in diabetic patients. Int J Control. 2020; 94:3054-67. [DOI:10.1080/00207179.2020.1750705]
- Alam W, Khan Q, Ali Riaz R, Akmeliawati R. Glucose–insulin stabilization in type-1 diabetic patient: A uniform exact differentiator–based robust integral sliding mode control approach. Int J Distrib Sens Netw. 2019; 15(3):ePub. [DOI:10.1177/1550147719833573]
- Heydarinejad H, Delavari H, Baleanu D. Fuzzy type-2 fractional Backstepping blood glucose control based on sliding mode observer. Int J Dynamics Control. 2019; 7(1):341-54. [DOI:10.1007/s40435-018-0445-8]
- Vakili S, ToosianShandiz H. Back-stepping sliding mode control design for glucose regulation in type 1 diabetic patients. Int J Nonlinear Anal Appl. 2019; 10(2):167-76. [DOI:10.22075/IJNAA.2019.4183]
- Balochian S, Alikhani Gr. Blood glucose adaptive generalized predictive control for critical care patients. Çankaya Univ J Human Soc Sci. 2019; 16:16-31. [Link]
- Vakili S, Toosian Shandiz H. Fractional order glucose insulin system using fractional back-stepping sliding mode control. Int J Nonlinear Anal Appl. 2019; 10(2):1-10. [DOI:10.22075/ijnaa.2019.4067]
- N’doye I, Voos H, Darouach M, Schneider JG. Static output the X∞ static for a fractional-order glucose-insulin system. Int J Control, Automat Syst. 2015; 13:798-807. [DOI:10.1007/s12555-013-9192-y]
- Petráš I. A note on the fractional-order Volta’s system. Commun Nonlinear Sci Numer Simul. 2010; 15(2):384-93. [DOI:10.1016/j.cnsns.2009.04.009]
- Deng W. Short memory principle and a predictor-corrector approach for fractional differential equations. J Comput Appl Math. 2007; 206(1):174-88. [DOI:10.1016/j.cam.2006.06.008]
- Li Y, Chen YQ, Podlubny I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput Math Appl. 2010; 59(5):1810-21. [DOI:10.1016/j.camwa.2009.08.019]
Type of Study: Orginal Article |
Subject:
● Psychosocial Health
Received: 2022/04/17 | Accepted: 2022/08/15 | Published: 2022/10/30
Received: 2022/04/17 | Accepted: 2022/08/15 | Published: 2022/10/30
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |








.jpg)
.jpg)
.jpg)