Volume 14, Issue 1 (Jan & Feb 2024)
J Research Health 2024, 14(1): 93-102 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Rezaei Nezhad H, Keynia F, Sabagh Mola Hoseini A. Estimating Algorithms for Prediction and Spread of a Factor as a Pandemic: A Case Study of Global COVID-19 Prevalence. J Research Health 2024; 14 (1) :93-102
URL: http://jrh.gmu.ac.ir/article-1-2118-en.html
URL: http://jrh.gmu.ac.ir/article-1-2118-en.html
1- Department of Computer, Faculty of Engineering, Kerman Branch, Islamic Azad University, Kerman, Iran.
2- Department of Energy Management and Optimization, Institute of Science and High Technology and Environmental Sciences, University of Advanced Technology, Kerman, Iran. ,f.keynia@kgut.ac.ir
3- School of Electronics, Electrical Engineering and Computer Science, Queen's University Belfast, Belfast, United Kingdom.
2- Department of Energy Management and Optimization, Institute of Science and High Technology and Environmental Sciences, University of Advanced Technology, Kerman, Iran. ,
3- School of Electronics, Electrical Engineering and Computer Science, Queen's University Belfast, Belfast, United Kingdom.
Full-Text [PDF 2121 kb]
(664 Downloads)
| Abstract (HTML) (2559 Views)
Full-Text: (965 Views)
Introduction
Apandemic is an epidemic of a disease that has exceeded the borders of several continents [1]. This is also called a global epidemic. Throughout history, several pandemics exist, the most well-known of which are smallpox, tuberculosis, and cholera [2]. One of the most horrific pandemics was the Black Death, also known as the plague, which killed 75–200 million people in the 14th century [3]. Diseases, such as AIDS and COVID-19 are examples of the pandemic in the current era [4]. Before the COVID-19 pandemic, one of the most famed pandemics in modern times was the 2009 swine flu outbreak. A pandemic is an epidemic that transcends international borders and affects a large number of people [5].
COVID-19 was first identified in Wuhan, Hubei Province, China in December 2019. So far, more than 200 countries and territories have been affected by the disease, with major outbreaks occurring in China, Iran, the United States, Italy, and Spain [6]. On March 11, 2020, the World Health Organization (WHO) declared COVID-19 a pandemic [7].
Various border controls have been implemented to contain the global COVID-19 pandemic, including airport detection and travel restrictions in several countries [8]. Computer modeling may help scientists project the virus spread among people; therefore, they can design a more effective plan to control them.
In the research, they found that calculations may have reduced the spread ratio of mainland China to other countries, but were insufficient to contain the global expansion of COVID-19. As most cases were spread during the asymptomatic induction period, our results suggest that fast-tracking of transmissions within the hotspots and at import sites is necessary to restrict human-to-human transmission outside mainland China [9].
One way to predict the dynamic outbreak of an epidemic is to use computer simulations following the mathematical model of an epidemic. In the literature, several analytical methods for epidemic modeling have been proposed, including the suspectable-infected-removed (SIR) model, the suspectable-exposed-infected-removed (SEIR) model, the susceptible-infectious-recovered-deceased susceptible infected recovered dead (SIRD) model, and SEIR and susceptible-exposed-infected-recovered-deceased (SEIRD) derivative fractions models [10].
While some recent studies have addressed this epidemic with the development of simulation codes, the need to develop open-source computer programs to simulate the dynamic spread time of the virus is intensely felt [11]. A reputable reference, called CHIME (COVID-19 hospital impact model for epidemics), also offers a Python-based program for hospital use. It is of paramount value to provide tutorial programs that demonstrate a mathematical model of the virus outbreak by the encrypted scripts in a block diagram [12, 13].
To analyze the recent deadly pandemic severe acute respiratory syndrome coronavirus 2 (Sars-Cov-2), the mathematical model containing the whole population is partitioned into five different compartments, represented by the SEIQR model. This current model especially contains the quarantined class and the immunity loss factor [14]. The basic reproduction that indicates the behavior of the disease is also estimated by the use of the next-generation matrix method [15]. A numerical simulation of this model is provided, the results are analyzed by theoretically strong numerical methods, and the known computational tool MATLAB Simulink R2020b is also used to visualize the results. Validation of results by MATLAB Simulink R2020b and numerical methods shows that this model and adopted methodology are appropriate and accurate and can be used for further predictions on COVID-19 [16].
One of the broad platforms employed to examine the dynamic behavior of a system is simulation/MATLAB. It has been widely used by many academic researchers in various fields to simulate dynamic systems using time domain simulations. A dynamic system, such as the spread of COVID-19, can be mathematically modeled by either a set of differential equations or a set of differential-algebraic equations depending on the model used. The main challenge with such simulations is to estimate the parameters in the model. For example, the rate of infection and recovery for a SIR model are the two input parameters to the model, while the model outputs are system state variables. The force of infection can be estimated from one of the models used in epidemiology, multiple models are used in epidemiology to simulate the forecasting and the spreading of a specific pandemic, some use fractional derivatives and others use ordinary differential equations, some with vaccination, and some with deceased cases. The definition and derivation of the first epidemic model, which is the SIR (susceptible cases of the disease, infectious cases of the disease, recovered cases of the disease) model, was by Kermack [17] and the models derived from this model were used to forecast lots of diseases, such as Ebola virus spread as Osemwinyen, Kamara, and Zhu, and with vaccination as [18].
Since only preliminary data exist to compare (confirmed cases of reported infection), the parameters of infection rate and the recovery rate can be estimated, such that the two outputs (reported and simulated cases) are equal and the difference is as close to zero as possible. However, parameter estimation may fail in many cases due to limitations imposed on the parameter, unknown initial values of the parameters, and or sudden surges in the reported data [11].
One observation of the proposed models in the literature is that the exponential function mathematically is a major part of the estimation. This is because the problem is nonlinear and the exponential function can show rates of increase or decrease depending on the sign and the exponent. When a plethora of dynamic changes is observed in data on the reported case or another wave of pandemic emerges, a challenge arises as simulation attempts to accurately track the data and estimate imminent outbreaks.
This requires variable inputs with multi-step functions to change their parameters whenever the changes in data rates are significant. Through this strategy, the program can solve the problem even when the infection data changes its level at different levels.
Another study revealed that consecutive travel restrictions to Wuhan, China reduced the disease transmission rate by 81% and 71% as of February 15, 2020, compared to no border restrictions. Border controls are hence unlikely to be involved in the pandemic but can delay the release of COVID-19 cases at an early stage of release [12].
Less than two months since the first international reports on COVID-19 in China, international flights spread the initial cases to 26 countries. For example, on February 21, 2020, these countries reported 556 confirmed cases. To this end, airport controlling and monitoring has attained particular importance to limit the global spread of COVID-19, the crucial method of its transmission which is to travel to this country and return directly or indirectly to the country of origin.
Therefore, the diagnosis of the symptoms of incoming passengers at airports has been implemented in several countries, and therefore it is clear that given the incubation period may last up to 14 days, a large portion of the incoming passengers are not identified as they do not exhibit the symptoms of the disease. For this reason, in setting our forecast model, two scenarios are considered for individuals with symptoms, namely the first therapeutic visit and hospitalization.
This paper was conducted to present open-source computer simulation programs developed to simulate, track, and estimate the COVID-19 outbreak. For this reason, in this research, this issue is analyzed and explored using software.
Methods
In this research, using various open-source programs, a method was proposed to track and estimate the spread of the virus around the globe in a simplified, efficient, and fast method. The proposed method is implemented using SIR and SEIR model models and coded under Simulink/MATLAB R2020b.
Points are automatically extracted from the data according to various statistics when data change dynamically. The number of exponential branches for rate functions remains up for the user’s selection because each data has its own specific needs from the parameters. The data is extracted from a valid source and is updated daily for all countries of the world. The user enters the country name as the input and executes the model with optional adjustable settings. Using an adaptive neuro-fuzzy inference system (ANFIS), the outbreak in China was simulated in Simulink, as the site where it was first identified and as the case study model for Asia, and the outbreak in Italy, as a case study in Europe using both standard mathematical models and the ANFIS.
Proposed model
Since the procedure developed in this paper aims to simulate any outbreak with potentially multiple dynamic changes in reported cases, an approach that applies to all possible scenarios is highly desirable. The reported data used for comparison are confirmed and measured as daily infection cases (m) or cumulative cases of infections (cm). These are nonlinear curves and can be represented by an exponential formula, such as Equation 1:

Where a denotes the increasing exponent that can be positive and negative, and c is a time constant. Regardless of the signs of the parameters representing physical components, the aforementioned function is always positive. When a notable change is observed in the reported data, the sigmoid function adapts its value to achieve new values for the parameters. In other words, the proposed rate function includes several branches of sigmoid functions. Each of them has a different increase and time constant. The aggregation final rate function of these functions is a branch as expressed in Equation 2 [5].

Where g is the gain of the branch, and for simplicity, the parameter a is assumed to be constant for estimation. The time parameter of c is represented by a vector whose elements can be manually selected or estimated. The length of this vector represents the branches of the sigmoid function, i.e. the iteration in the rate function (Equation 2). The culminating sigmoid function can be further generalized by subtracting the function of the previous sigmoid from what is intended. The following rate function is used for the latter concept with a generalized/improvement rate function to track the problem. The greater the number of branches (n), the smoother and better the correspondence between the reported data and the simulated graph.

For the estimation problem, the above function should be multiplied by an exponent component with a negative sign to reduce the curve if the epidemic has not yet passed its peak. Parameters other than the new components are also estimated by the solver. If the power is zero, the function will be as the Equation 3. However, each non-zero representative leads to different case studies, such as standard, upper-bound, and lower-bound estimates. The Equation 4 can be used to estimate the parameters with any optional scenario.
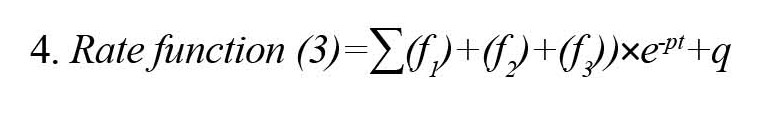
Where q and p, are parameters to be estimated. Since the recovery function, unlike the infection function, has a constant change rate given the lack of vaccine at present, this function can be represented with only a sigmoid function or even more simply as a fixed parameter. It is worth noting by the program that if a=0 in the rate function, the sigmoid functions become a sum-step function. The lower the exponent of the sigmoid function, the steeper the curve, and vice versa.
Illustrates the proposed concept for different values of a, where S in the figure refers to a step function. For the initial values of the parameters, a method that satisfies all potential outbreaks is required. An efficient method is to use a confirmed infection ratio (lm [t]/lm [t-1]) and normalize the ratio in the range between zero and one. This value is used for the gain parameters of sigmoid branches, i.e. g in Equation 2 for temporal parameters. Therefore, one of the following methods can be employed to this end, and due to its generality and simplicity, the second method is considered the standard method of programs. In MATLAB R2020b, a function called “MaxNumChanges” is provided to determine some useful statistical information with the Linear relation (𝑙𝑖𝑛𝑒𝑎𝑟), Root-mean square relationship (RMS) and Semantic Mean±SD. The first technique is considered an elementary tool to determine the initial time, but it can be easily renamed to other techniques by changing its name. Figure 1 shows these concepts assuming maximum variations of 2, 3, 5, and 10. Increasing this value provides better output matching and parameter estimation. In many cases, it has been reported that 3-5 changes (also representing the number of sigmoid branches) are sufficient for this problem. However, it remains for the user to select the number of change points to adjust the estimate for each outbreak.
3. Results
To evaluate the proposed model, 2-5 shows some results obtained from the coronavirus outbreak in Iran, Iraq, Turkey, Afghanistan, China, and England for estimation. This outbreak was chosen due to the many dynamic changes in the number of reported cases to demonstrate the ability of the programs to simulate such a problem. As shown in the Figures, the programs can be used to simulate epidemics in different scenarios and confidence intervals at different times. By applying new measures, it is easy to see the effect of these control efforts in future estimates.
Detailed models (suspectable-exposed-infected-removed [SEIR], susceptible infected recovered dead [SIRD], and susceptible-exposed-infected-recovered-deceased [SEIRD]).
As explained above, the above model does not provide information about people at risk of infection who have not yet been identified simply because they are yet to be confirmed. It also does not provide any information on closed cases of infected people who have died. An exposed variable can be added to the SIR model to form a SEIR model of recovery, while an end variable (death) can also be added to the SEIR model to form the SEIRD model. This model is more general and is accepted in this section. The differential Equations of this model are as follows (Equations 5-9):
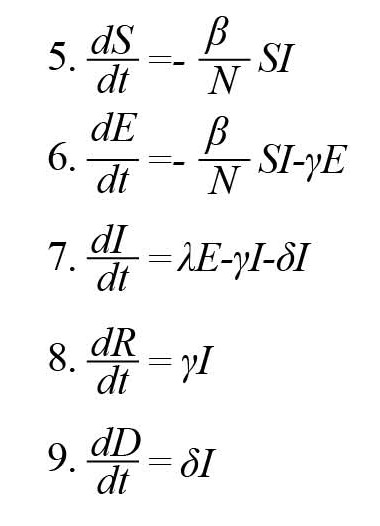
Where E refers to the exposed state variable, D denotes the deceased population. The sum of the above relations (8, 9) must be zero while the sum of the state variables must be constant and equal to the population: N=S+E+I+R+D
Several applications are added to Sigmoid, including SEIR, SEIRD, and SEIRD, designed and coded in Simulink and MATLAB. It is noteworthy that the actual data collected should be used as input to this model. This data is stored in Excel spreadsheets and a block in Simulink allows us to import data from external sources and generate a custom signal.
This block is called a “signal generator”. The ratio between daily deaths and daily infections is used to indicate mortality. This signal is a real data-based signal that is multiplied by a simulated infectious signal to integrate and form a cumulative dead variable using an integral block in Simulink. In the Figure 2, orange is used for the “exposed” and dark red is used for the “dead” compartments. The process of optimizing the parameters and numerical outputs is not depicted here due to its similarity to the SIR model. This section aims to show how to configure and edit the SIR model to build a new model. Therefore, in the initial design of this model, a set of step functions was used instead of sigmoid functions to provide more normal diagrams.
Simulation with control measures
Complete or partial lockdown, social distancing, and controlling sporting conditions can affect the spread of the virus, and if these steps are applied in advance, the corresponding curve is flattened sooner. In the Simulink model, all these control actions can be represented, and hence simulated, using a step function (or sigmoid function). These controls affect the rate of infection and reduce beta function. On the other hand, the production of a vaccine or the inclusion of other methods to improve or reduce the rate of disease (such as providing all the necessary ventilation equipment for hospitals) affects the parameter of the recovery rate. As a result, with each change in these two parameters, the reproduction ratio decreases and the effect of response delay on the curve is also readily evident in Simulink. This can be achieved by adding a delay block to the infection function. Therefore, more details about the model are needed for this problem.
The educational value of simCOVID
SimCOVID is an open-source package used to simulate, track, and estimate an outbreak that comes with editable files and codes. The MATLAB programs were simply coded; only one main script exists for everything (reading data, parameter estimation, solving DEs, and plotting). The data itself comes from the source as an Excel sheet. A generalized method is adopted to reduce the user’s actions to solve the problem. Changing the model from one to another is also straightforward; the new equations, initial values, and their limits are appended to the existing equations. After optimizing the parameters, the adaptive neuro-fuzzy inference system toolbox is used to generate seven fuzzy rules for each output. The membership function used in this training is the Gaussian function.
Discussion
This study was conducted to present an open-source toolbox to model, simulate, and estimate the outbreak of COVID-19.
The models used in the previous sections were based on the mathematical model of the problem. It is also possible to build a machine learning procedure to simulate the same system using model input and output data. Simulink provides the user with a neural-fuzzy adaptive toolbox to automatically generate fuzzy rules based on the data training. Lin et al. provide a detailed explanation of the technique in which the same method is employed. Using a basic SIR model built into Simulink with variable infection rates and constant recovery rates, the model is taught using input data [13].
Input can be the infection rate, the recovery rate, or a combination of both in Figure 10. The output can be the infected or its cumulative function. In the present study, the beta function and its derivative are used as input variables to the ANFIS model, while variables for infectious and cumulative cases are selected for output in two different training processes. The ANFIS model makes it possible to use only one output for each block. Two separate processes should be employed to generate two blocks of ANFIS for two outputs. More outputs require more ANFIS blocks [14]. Recovery performance is constant as proposed in the study [10], while infection rate is defined as a treatment variable.
By optimizing the parameters, the ANFIS toolbox is used to generate seven fuzzy rules for each output. The membership function used in this training procedure is the Gaussian function Figure 2, Figure 3, Figure 4 and Figure 5, demonstrate the training iterations, fuzzy rules, and output of the ANFIS model for cumulative and infectious variables, respectively. Figure 3 shows the Simulink model for the ANFIS blocks in this simulation. These rules, if used, are used to simulate COVID-19 outbreaks in China, the results of which are shown in Figure 4 and Figure 5 plot the values of infection and recovery parameters that produce acceptable output results, which can also be enriched or improved in a process known as updating. The beta function can be used in more detail and complexity to improve the accuracy and efficiency of the result-extraction procedure [15].
Conclusion
The present study was conducted to present an open-source toolbox to model, simulate, and estimate the outbreak of COVID-19. This procedure is presented in such a way that it can be generalized and applied in other applications on estimating the scenarios of an event, including the potential of several models. Furthermore, several statistical procedures were employed to determine the optimal time parameters for sigmoid functions. In addition, an ANFIS was used to generate model output based on some of the training tasks applied to the system. This article promises some lasting contributions to the field of COVID-19. This program can be used as an educational tool or for research studies.
Ethical Considerations
Compliance with ethical guidelines
Questionnaires were filled with the participants’ satisfaction and written consent was obtained from the participants in this study (07/25/10001/10866).
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
Conceptualization, study design, data analysis, data interpretation and drafting the manuscript: Hamideh Rezaei Nezhad and Farshid Keynia; Data acquisition: Amir Sabbagh Molahosseini; Review, editing and final approval: All authors.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
The authors appreciate all participants in the study.
References
Apandemic is an epidemic of a disease that has exceeded the borders of several continents [1]. This is also called a global epidemic. Throughout history, several pandemics exist, the most well-known of which are smallpox, tuberculosis, and cholera [2]. One of the most horrific pandemics was the Black Death, also known as the plague, which killed 75–200 million people in the 14th century [3]. Diseases, such as AIDS and COVID-19 are examples of the pandemic in the current era [4]. Before the COVID-19 pandemic, one of the most famed pandemics in modern times was the 2009 swine flu outbreak. A pandemic is an epidemic that transcends international borders and affects a large number of people [5].
COVID-19 was first identified in Wuhan, Hubei Province, China in December 2019. So far, more than 200 countries and territories have been affected by the disease, with major outbreaks occurring in China, Iran, the United States, Italy, and Spain [6]. On March 11, 2020, the World Health Organization (WHO) declared COVID-19 a pandemic [7].
Various border controls have been implemented to contain the global COVID-19 pandemic, including airport detection and travel restrictions in several countries [8]. Computer modeling may help scientists project the virus spread among people; therefore, they can design a more effective plan to control them.
In the research, they found that calculations may have reduced the spread ratio of mainland China to other countries, but were insufficient to contain the global expansion of COVID-19. As most cases were spread during the asymptomatic induction period, our results suggest that fast-tracking of transmissions within the hotspots and at import sites is necessary to restrict human-to-human transmission outside mainland China [9].
One way to predict the dynamic outbreak of an epidemic is to use computer simulations following the mathematical model of an epidemic. In the literature, several analytical methods for epidemic modeling have been proposed, including the suspectable-infected-removed (SIR) model, the suspectable-exposed-infected-removed (SEIR) model, the susceptible-infectious-recovered-deceased susceptible infected recovered dead (SIRD) model, and SEIR and susceptible-exposed-infected-recovered-deceased (SEIRD) derivative fractions models [10].
While some recent studies have addressed this epidemic with the development of simulation codes, the need to develop open-source computer programs to simulate the dynamic spread time of the virus is intensely felt [11]. A reputable reference, called CHIME (COVID-19 hospital impact model for epidemics), also offers a Python-based program for hospital use. It is of paramount value to provide tutorial programs that demonstrate a mathematical model of the virus outbreak by the encrypted scripts in a block diagram [12, 13].
To analyze the recent deadly pandemic severe acute respiratory syndrome coronavirus 2 (Sars-Cov-2), the mathematical model containing the whole population is partitioned into five different compartments, represented by the SEIQR model. This current model especially contains the quarantined class and the immunity loss factor [14]. The basic reproduction that indicates the behavior of the disease is also estimated by the use of the next-generation matrix method [15]. A numerical simulation of this model is provided, the results are analyzed by theoretically strong numerical methods, and the known computational tool MATLAB Simulink R2020b is also used to visualize the results. Validation of results by MATLAB Simulink R2020b and numerical methods shows that this model and adopted methodology are appropriate and accurate and can be used for further predictions on COVID-19 [16].
One of the broad platforms employed to examine the dynamic behavior of a system is simulation/MATLAB. It has been widely used by many academic researchers in various fields to simulate dynamic systems using time domain simulations. A dynamic system, such as the spread of COVID-19, can be mathematically modeled by either a set of differential equations or a set of differential-algebraic equations depending on the model used. The main challenge with such simulations is to estimate the parameters in the model. For example, the rate of infection and recovery for a SIR model are the two input parameters to the model, while the model outputs are system state variables. The force of infection can be estimated from one of the models used in epidemiology, multiple models are used in epidemiology to simulate the forecasting and the spreading of a specific pandemic, some use fractional derivatives and others use ordinary differential equations, some with vaccination, and some with deceased cases. The definition and derivation of the first epidemic model, which is the SIR (susceptible cases of the disease, infectious cases of the disease, recovered cases of the disease) model, was by Kermack [17] and the models derived from this model were used to forecast lots of diseases, such as Ebola virus spread as Osemwinyen, Kamara, and Zhu, and with vaccination as [18].
Since only preliminary data exist to compare (confirmed cases of reported infection), the parameters of infection rate and the recovery rate can be estimated, such that the two outputs (reported and simulated cases) are equal and the difference is as close to zero as possible. However, parameter estimation may fail in many cases due to limitations imposed on the parameter, unknown initial values of the parameters, and or sudden surges in the reported data [11].
One observation of the proposed models in the literature is that the exponential function mathematically is a major part of the estimation. This is because the problem is nonlinear and the exponential function can show rates of increase or decrease depending on the sign and the exponent. When a plethora of dynamic changes is observed in data on the reported case or another wave of pandemic emerges, a challenge arises as simulation attempts to accurately track the data and estimate imminent outbreaks.
This requires variable inputs with multi-step functions to change their parameters whenever the changes in data rates are significant. Through this strategy, the program can solve the problem even when the infection data changes its level at different levels.
Another study revealed that consecutive travel restrictions to Wuhan, China reduced the disease transmission rate by 81% and 71% as of February 15, 2020, compared to no border restrictions. Border controls are hence unlikely to be involved in the pandemic but can delay the release of COVID-19 cases at an early stage of release [12].
Less than two months since the first international reports on COVID-19 in China, international flights spread the initial cases to 26 countries. For example, on February 21, 2020, these countries reported 556 confirmed cases. To this end, airport controlling and monitoring has attained particular importance to limit the global spread of COVID-19, the crucial method of its transmission which is to travel to this country and return directly or indirectly to the country of origin.
Therefore, the diagnosis of the symptoms of incoming passengers at airports has been implemented in several countries, and therefore it is clear that given the incubation period may last up to 14 days, a large portion of the incoming passengers are not identified as they do not exhibit the symptoms of the disease. For this reason, in setting our forecast model, two scenarios are considered for individuals with symptoms, namely the first therapeutic visit and hospitalization.
This paper was conducted to present open-source computer simulation programs developed to simulate, track, and estimate the COVID-19 outbreak. For this reason, in this research, this issue is analyzed and explored using software.
Methods
In this research, using various open-source programs, a method was proposed to track and estimate the spread of the virus around the globe in a simplified, efficient, and fast method. The proposed method is implemented using SIR and SEIR model models and coded under Simulink/MATLAB R2020b.
Points are automatically extracted from the data according to various statistics when data change dynamically. The number of exponential branches for rate functions remains up for the user’s selection because each data has its own specific needs from the parameters. The data is extracted from a valid source and is updated daily for all countries of the world. The user enters the country name as the input and executes the model with optional adjustable settings. Using an adaptive neuro-fuzzy inference system (ANFIS), the outbreak in China was simulated in Simulink, as the site where it was first identified and as the case study model for Asia, and the outbreak in Italy, as a case study in Europe using both standard mathematical models and the ANFIS.
Proposed model
Since the procedure developed in this paper aims to simulate any outbreak with potentially multiple dynamic changes in reported cases, an approach that applies to all possible scenarios is highly desirable. The reported data used for comparison are confirmed and measured as daily infection cases (m) or cumulative cases of infections (cm). These are nonlinear curves and can be represented by an exponential formula, such as Equation 1:

Where a denotes the increasing exponent that can be positive and negative, and c is a time constant. Regardless of the signs of the parameters representing physical components, the aforementioned function is always positive. When a notable change is observed in the reported data, the sigmoid function adapts its value to achieve new values for the parameters. In other words, the proposed rate function includes several branches of sigmoid functions. Each of them has a different increase and time constant. The aggregation final rate function of these functions is a branch as expressed in Equation 2 [5].

Where g is the gain of the branch, and for simplicity, the parameter a is assumed to be constant for estimation. The time parameter of c is represented by a vector whose elements can be manually selected or estimated. The length of this vector represents the branches of the sigmoid function, i.e. the iteration in the rate function (Equation 2). The culminating sigmoid function can be further generalized by subtracting the function of the previous sigmoid from what is intended. The following rate function is used for the latter concept with a generalized/improvement rate function to track the problem. The greater the number of branches (n), the smoother and better the correspondence between the reported data and the simulated graph.

For the estimation problem, the above function should be multiplied by an exponent component with a negative sign to reduce the curve if the epidemic has not yet passed its peak. Parameters other than the new components are also estimated by the solver. If the power is zero, the function will be as the Equation 3. However, each non-zero representative leads to different case studies, such as standard, upper-bound, and lower-bound estimates. The Equation 4 can be used to estimate the parameters with any optional scenario.
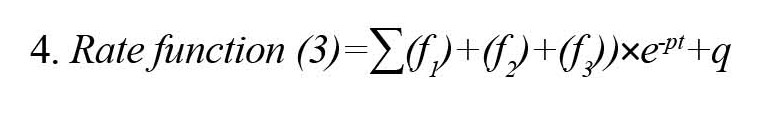
Where q and p, are parameters to be estimated. Since the recovery function, unlike the infection function, has a constant change rate given the lack of vaccine at present, this function can be represented with only a sigmoid function or even more simply as a fixed parameter. It is worth noting by the program that if a=0 in the rate function, the sigmoid functions become a sum-step function. The lower the exponent of the sigmoid function, the steeper the curve, and vice versa.
Illustrates the proposed concept for different values of a, where S in the figure refers to a step function. For the initial values of the parameters, a method that satisfies all potential outbreaks is required. An efficient method is to use a confirmed infection ratio (lm [t]/lm [t-1]) and normalize the ratio in the range between zero and one. This value is used for the gain parameters of sigmoid branches, i.e. g in Equation 2 for temporal parameters. Therefore, one of the following methods can be employed to this end, and due to its generality and simplicity, the second method is considered the standard method of programs. In MATLAB R2020b, a function called “MaxNumChanges” is provided to determine some useful statistical information with the Linear relation (𝑙𝑖𝑛𝑒𝑎𝑟), Root-mean square relationship (RMS) and Semantic Mean±SD. The first technique is considered an elementary tool to determine the initial time, but it can be easily renamed to other techniques by changing its name. Figure 1 shows these concepts assuming maximum variations of 2, 3, 5, and 10. Increasing this value provides better output matching and parameter estimation. In many cases, it has been reported that 3-5 changes (also representing the number of sigmoid branches) are sufficient for this problem. However, it remains for the user to select the number of change points to adjust the estimate for each outbreak.
3. Results
To evaluate the proposed model, 2-5 shows some results obtained from the coronavirus outbreak in Iran, Iraq, Turkey, Afghanistan, China, and England for estimation. This outbreak was chosen due to the many dynamic changes in the number of reported cases to demonstrate the ability of the programs to simulate such a problem. As shown in the Figures, the programs can be used to simulate epidemics in different scenarios and confidence intervals at different times. By applying new measures, it is easy to see the effect of these control efforts in future estimates.
Detailed models (suspectable-exposed-infected-removed [SEIR], susceptible infected recovered dead [SIRD], and susceptible-exposed-infected-recovered-deceased [SEIRD]).
As explained above, the above model does not provide information about people at risk of infection who have not yet been identified simply because they are yet to be confirmed. It also does not provide any information on closed cases of infected people who have died. An exposed variable can be added to the SIR model to form a SEIR model of recovery, while an end variable (death) can also be added to the SEIR model to form the SEIRD model. This model is more general and is accepted in this section. The differential Equations of this model are as follows (Equations 5-9):
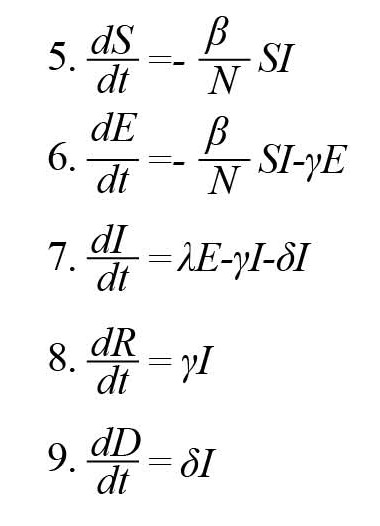
Where E refers to the exposed state variable, D denotes the deceased population. The sum of the above relations (8, 9) must be zero while the sum of the state variables must be constant and equal to the population: N=S+E+I+R+D
Several applications are added to Sigmoid, including SEIR, SEIRD, and SEIRD, designed and coded in Simulink and MATLAB. It is noteworthy that the actual data collected should be used as input to this model. This data is stored in Excel spreadsheets and a block in Simulink allows us to import data from external sources and generate a custom signal.
This block is called a “signal generator”. The ratio between daily deaths and daily infections is used to indicate mortality. This signal is a real data-based signal that is multiplied by a simulated infectious signal to integrate and form a cumulative dead variable using an integral block in Simulink. In the Figure 2, orange is used for the “exposed” and dark red is used for the “dead” compartments. The process of optimizing the parameters and numerical outputs is not depicted here due to its similarity to the SIR model. This section aims to show how to configure and edit the SIR model to build a new model. Therefore, in the initial design of this model, a set of step functions was used instead of sigmoid functions to provide more normal diagrams.
Simulation with control measures
Complete or partial lockdown, social distancing, and controlling sporting conditions can affect the spread of the virus, and if these steps are applied in advance, the corresponding curve is flattened sooner. In the Simulink model, all these control actions can be represented, and hence simulated, using a step function (or sigmoid function). These controls affect the rate of infection and reduce beta function. On the other hand, the production of a vaccine or the inclusion of other methods to improve or reduce the rate of disease (such as providing all the necessary ventilation equipment for hospitals) affects the parameter of the recovery rate. As a result, with each change in these two parameters, the reproduction ratio decreases and the effect of response delay on the curve is also readily evident in Simulink. This can be achieved by adding a delay block to the infection function. Therefore, more details about the model are needed for this problem.
The educational value of simCOVID
SimCOVID is an open-source package used to simulate, track, and estimate an outbreak that comes with editable files and codes. The MATLAB programs were simply coded; only one main script exists for everything (reading data, parameter estimation, solving DEs, and plotting). The data itself comes from the source as an Excel sheet. A generalized method is adopted to reduce the user’s actions to solve the problem. Changing the model from one to another is also straightforward; the new equations, initial values, and their limits are appended to the existing equations. After optimizing the parameters, the adaptive neuro-fuzzy inference system toolbox is used to generate seven fuzzy rules for each output. The membership function used in this training is the Gaussian function.
Discussion
This study was conducted to present an open-source toolbox to model, simulate, and estimate the outbreak of COVID-19.
The models used in the previous sections were based on the mathematical model of the problem. It is also possible to build a machine learning procedure to simulate the same system using model input and output data. Simulink provides the user with a neural-fuzzy adaptive toolbox to automatically generate fuzzy rules based on the data training. Lin et al. provide a detailed explanation of the technique in which the same method is employed. Using a basic SIR model built into Simulink with variable infection rates and constant recovery rates, the model is taught using input data [13].
Input can be the infection rate, the recovery rate, or a combination of both in Figure 10. The output can be the infected or its cumulative function. In the present study, the beta function and its derivative are used as input variables to the ANFIS model, while variables for infectious and cumulative cases are selected for output in two different training processes. The ANFIS model makes it possible to use only one output for each block. Two separate processes should be employed to generate two blocks of ANFIS for two outputs. More outputs require more ANFIS blocks [14]. Recovery performance is constant as proposed in the study [10], while infection rate is defined as a treatment variable.
By optimizing the parameters, the ANFIS toolbox is used to generate seven fuzzy rules for each output. The membership function used in this training procedure is the Gaussian function Figure 2, Figure 3, Figure 4 and Figure 5, demonstrate the training iterations, fuzzy rules, and output of the ANFIS model for cumulative and infectious variables, respectively. Figure 3 shows the Simulink model for the ANFIS blocks in this simulation. These rules, if used, are used to simulate COVID-19 outbreaks in China, the results of which are shown in Figure 4 and Figure 5 plot the values of infection and recovery parameters that produce acceptable output results, which can also be enriched or improved in a process known as updating. The beta function can be used in more detail and complexity to improve the accuracy and efficiency of the result-extraction procedure [15].
Conclusion
The present study was conducted to present an open-source toolbox to model, simulate, and estimate the outbreak of COVID-19. This procedure is presented in such a way that it can be generalized and applied in other applications on estimating the scenarios of an event, including the potential of several models. Furthermore, several statistical procedures were employed to determine the optimal time parameters for sigmoid functions. In addition, an ANFIS was used to generate model output based on some of the training tasks applied to the system. This article promises some lasting contributions to the field of COVID-19. This program can be used as an educational tool or for research studies.
Ethical Considerations
Compliance with ethical guidelines
Questionnaires were filled with the participants’ satisfaction and written consent was obtained from the participants in this study (07/25/10001/10866).
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
Conceptualization, study design, data analysis, data interpretation and drafting the manuscript: Hamideh Rezaei Nezhad and Farshid Keynia; Data acquisition: Amir Sabbagh Molahosseini; Review, editing and final approval: All authors.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
The authors appreciate all participants in the study.
References
- Mirshakari J. [Dictionary of words approved by the Academy (Persian)]. Sari: Asre Mandegar; 2010. [Link]
- Kampf G, Todt D, Pfaender S, Steinmann E. Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents. Journal of Hospital Infection. 2020; 104(3):246-51. [DOI:10.1016/j.jhin.2020.01.022] [PMID]
- Russell CD, Millar JE, Baillie JK. Clinical evidence does not support corticosteroid treatment for 2019-nCoV lung injury. Lancet. 2020; 395(10223):473-5. [DOI:10.1016/S0140-6736(20)30317-2] [PMID]
- Xu Z, Peng C, Shi Y, Zhu Z, Mu K, Wang X, et al. Nelfinavir was predicted to be a potential inhibitor of 2019-nCov main protease by an integrative approach combining homology modelling. molecular docking and binding free energy calculation. bioRxiv. 2020; 1-20. [DOI:10.1101/2020.01.27.921627]
- Mollania H. [Dynamic state estimator design in power system by considering prioritization for network nodes (Persian) ] [PhD dissertation]. Mashhad: Ferdowsi University of Mashhad; 2017.
- Li G, Fan Y, Lai Y, Han T, Li Z, Zhou P, et al. Coronavirus infections and immune responses. Journal of Medical Virology. 2020; 92(4):424-32. [DOI:10.1002/jmv.25685] [PMID]
- Saha A, Lee Y, Hwang Y, Psannis K, Kim B. Context-aware block-based motion estimation algorithm for multimedia internet of things (IoT) platform. Personal and Ubiquitous Computing. 2018; 22(1):163-72. [DOI:10.1007/s00779-017-1058-5]
- Abdulrahman I, Radman G. Wide-area-based adaptive neuro-fuzzy SVC controller for damping interarea oscillations. Canadian Journal of Electrical and Computer Engineering. 2018; 14(3):133-44. [DOI:10.1109/CJECE.2018.2868754]
- Esfandiari K, Abdollahi F, Talebi HA. A stable nonlinear in parameter neural network controller for a class of saturated nonlinear systems. IFAC Proceedings Volumes. 2014; 47(3): 2533-8. [DOI:10.3182/20140824-6-ZA-1003.00853]
- Zhong L, Mu L, Li J, Wang J, Yin Z, Liu D. Early prediction of the 2019 novel coronavirus outbreak in the mainland china based on simple Mathematical Model. IEEE Access. 2020; 8:51761-9. [DOI:10.1109/ACCESS.2020.2979599] [PMID]
- Mohammadi F, Kouzehgari S. [Predicting the prevalence of covid-19 and its mortality rate in Iran using lyapunov exponent (Persian)]. Journal of Inflammatory Diseases. 2020; 24(2):108-23. [DOI:10.32598/JQUMS.24.2.2415.1]
- Zahedi B. [A new algorithm for estimating channel and carrier frequency latency in wireless relay networks (Persian)] [MSc thesis]. Tehran: Khajeh Nasir al-Din Tusi University of Technology; 2011. [Link]
- Lin J,Wang F, Cai A, Yan W, Cui W, Mo J, Shao S. Daily load curve forecasting using factor analysis and RBF neural network based on load segmentation. Paper presented at: 2017 China International Electrical and Energy Conference (CIEEC). 25-27 October 2017; Beijing, China. [DOI:10.1109/CIEEC.2017.8388514]
- Caccavo D. Chinese and Italian COVID-19 outbreaks can be correctly described by a modified SIRD model. Pre-print manuscript. 2020; 1-13. [DOI:10.13140/RG.2.2.24485.86243]
- Peng L, Yang W, Zhang D, Zhuge C, Hong L. Epidemic analysis of COVID-19 in China by dynamical modeling. Preprint ar Xiv. 2020. [DOI:10.48550/arXiv.2002.06563]
- Abdulrahman I. SimCOVID: Open-source simulation program for the COVID-19 outbreak. SN Computer Science. 2023; 4(1):20. [PMID]
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemic. Proceedings of the Royal Society of London. Series A. 1927; 115:700-21. [DOI:10.1098/rspa.1927.0118]
- Al-Raeei M. Numerical simulation of the force of infection and the typical times of SARS-CoV-2 disease for different location countries. Modeling Earth Systems and Environment. 2022; 8(1):1443-8. [DOI:10.1007/s40808-020-01075-3] [PMID]
Type of Study: Case report |
Subject:
● International Health
Received: 2022/09/18 | Accepted: 2023/01/21 | Published: 2024/02/1
Received: 2022/09/18 | Accepted: 2023/01/21 | Published: 2024/02/1
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |